avl系统,自平衡二叉搜索树的奥秘

深入解析AVL树：自平衡二叉搜索树的奥秘

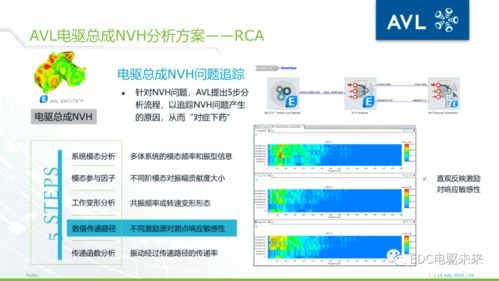
在计算机科学中，数据结构是构建高效算法的基础。AVL树作为一种自平衡二叉搜索树，因其高效的查询、插入和删除操作而备受关注。本文将深入解析AVL树的工作原理、实现方法以及在实际应用中的优势。

一、AVL树的定义与特点

AVL树是由G. M. Adelson-Velsky和E. M. Landis在1962年提出的自平衡二叉搜索树。它是一种特殊的二叉搜索树，其特点是任何节点的两个子树的高度最大差别为1。这种严格的平衡特性使得AVL树在查询、插入和删除操作中都能保持较高的效率。

二、AVL树的结构与性质

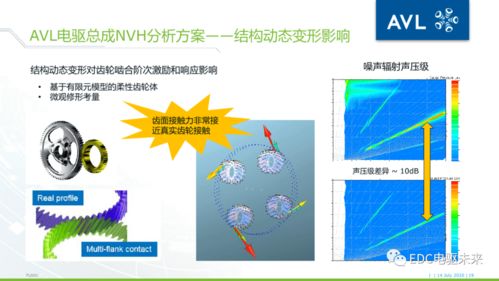
AVL树的结构与普通的二叉搜索树类似，但每个节点都包含一个额外的信息——平衡因子。平衡因子是节点左子树高度与右子树高度之差的绝对值。AVL树的平衡因子范围是-1、0和1，这意味着任何节点的左右子树高度差不会超过1。

AVL树具有以下性质：

每个节点都有一个平衡因子，且范围在-1、0和1之间。

AVL树是一个二叉搜索树，满足二叉搜索树的性质。

AVL树的任何子树也都是AVL树。

三、AVL树的插入操作

在AVL树中插入一个新节点时，首先按照二叉搜索树的规则进行插入。插入完成后，需要检查新节点及其祖先节点的平衡因子，以确定是否需要进行旋转操作来恢复树的平衡。

插入操作分为以下步骤：

按照二叉搜索树的规则插入新节点。

从插入节点开始向上遍历，计算每个节点的平衡因子。

如果某个节点的平衡因子绝对值大于1，则需要进行旋转操作来恢复树的平衡。

四、AVL树的旋转操作

AVL树的旋转操作是恢复树平衡的关键。旋转操作分为四种类型：左旋、右旋、左右旋和右左旋。以下分别介绍这四种旋转操作：

左旋（LL旋转）：当节点A的左子树高度大于右子树高度，且节点A的左子树的左子树高度也大于右子树高度时，进行左旋操作。

右旋（RR旋转）：当节点A的右子树高度大于左子树高度，且节点A的右子树的右子树高度也大于左子树高度时，进行右旋操作。

左右旋（LR旋转）：当节点A的左子树高度大于右子树高度，且节点A的左子树的右子树高度大于左子树高度时，进行左右旋操作。

右左旋（RL旋转）：当节点A的右子树高度大于左子树高度，且节点A的右子树的左子树高度大于右子树高度时，进行右左旋操作。

五、AVL树的应用与优势

AVL树因其高效的查询、插入和删除操作而被广泛应用于各种场景，如数据库索引、内存数据结构等。以下是AVL树的一些应用与优势：

数据库索引：AVL树可以用于构建数据库索引，提高查询效率。

内存数据结构：AVL树可以用于实现内存中的数据结构，如字典、集合等。

高效性：AVL树在查询、插入和删除操作中都能保持较高的效率，时间复杂度为O(log N)。

稳定性：AVL树始终保持平衡，不会出现退化成链表的情况。